 |
Institute for Theoretical Physics | |||||
statistical mechanics group|
leonardo
|
||||||
|
||||||
 |
Institute for Theoretical Physics | |||||
statistical mechanics group|
leonardo
|
||||||
|
||||||
 |
Kirsten Harth1, Ralf Stannarius1, Andreas
Hahn2, Lutz Tobiska2
1Institute of Experimental Physics,
Otto-von-Guericke University Magdeburg
2Institute of Analysis and Numerics,
Otto-von-Guericke University Magdeburg
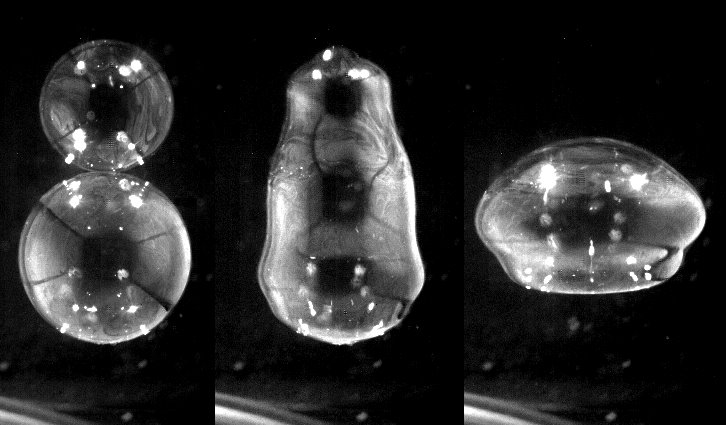
Shape transformations of liquid droplets in a gaseous environment or gas bubbles in fluids are of high technological importance, and they have attracted physicists' and mathematicians' interest since the days of Lord Kelvin. Everyone of us has been familiar with soap bubbles since early childhood days. These systems are extremely easy to prepare and to investigate. At the same time, they are perfectly suited as model systems for complex hydrodynamic problems.
When two smaller bubbles fuse to a larger one, the resulting bubbles undergoes shape oscillations until it reaches its new spherical equilibrium. An analytical solution for small ocillation amplitudes and inviscid materials has already been found by Sir Horace Lamb in the 19th century. Here, we deal with viscous fluids and large shape deformations, where no analytic solutions are available. In literature, a number of approximative solutions are discussed. We simulate the shape tranformation process using a two-phase mapped finite elements method on moveable meshes, implemented in MooNMD. The thin soap film is represented by its surface tension. For the inner and outer volumes of air, the Navier-Stokes-Equations are solved. Arbitrary initial configurations can be treated. We commonly start with experimental data or selected pre-defined shapes.
For further details on experimental data see Ref. 1, for a description of the program see Ref. 2.
 |
Steffen Harbich
Student at Otto-von-Guericke-University Magdeburg
Determining whether two graphs are isomorphic, i.e. whether two graphs have the same structure, is a well-known problem in mathematics and computer science. There are a numerous applications - for example in chemical mathematics - and a lot of fast algorithms for solving the problem in practice. But the complexity of the problem is still unknown: neither a polynomial time algorithm is known nor is the problem proven to be NP-complete. With the bachelor thesis "On Determining the Automorphisms of Graphs" (german title "Zur Bestimmung der Automorphismen von Graphen") a new algorithm is presented for the closely related problem of determining automorphisms of graphs which are isomorphisms of a graph to itself. The algorithm computes the solution of the graph isomorphism problem in polynomal time, but the correctness of the algorithm is not proven until now. Tina helps on testing that new algorithm for a large number of graphs.
 |
Stefan
Streif1,2,
Dieter Oesterhelt3,
and Wolfgang Marwan1,2
1Max Planck Institute for Dynamics of Complex Technical
Systems, Magdeburg, Germany
Molecular Network Analysis Group
2Otto-von-Guericke Universität Magdeburg, Institute for
Biology, Germany
3Max Planck Institute of Biochemistry, Martinsried,
Germany
Dept. for Membrane Biochemistry
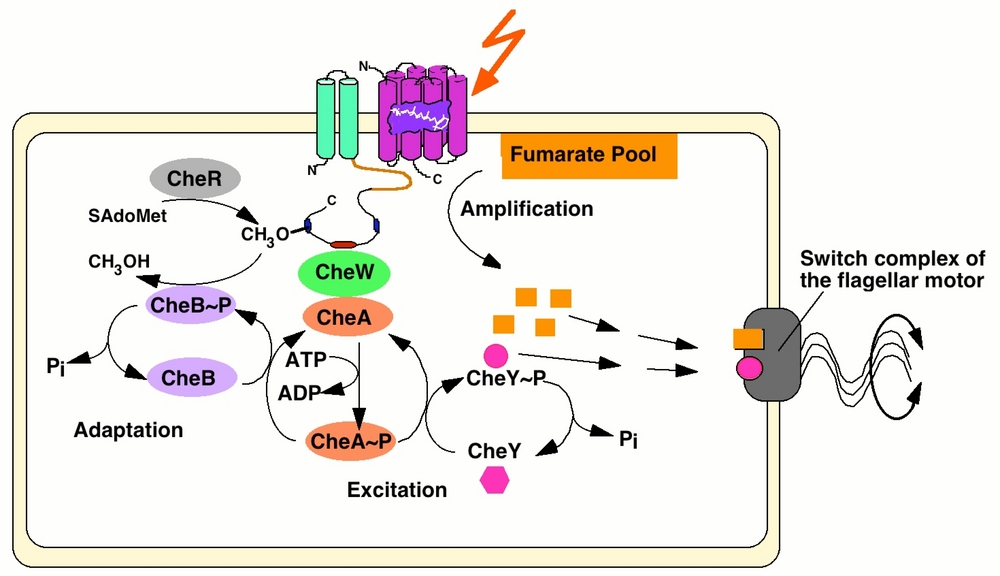
Halobacterium salinarum is a model organism for the halophilic branch of the archaea. It is rod-shaped, motile, lives in highly saline environments (4M salt and higher), and is one of the few species known that can live in saturated salt solutions.
H. salinarum cells respond to light, nutrients, and noxious chemicals by swimming to those places of their natural habitat that provide the best living conditions available at the moment.
Sensory receptors feed into a core signal processing network composed of 11 cytoplasmic proteins which mediates signal integration, adaptation and motor response. Because the network is small and many molecular details are known, mechanistic questions related to receptor activation, functional cross-talk of receptors, or the biophysical chemistry of signal processing can be addressed at the single cell level.
A kinetic model of the signal processing network quantitatively predicts the cellular response to complex patterns of light stimulation, and the spontaneous behaviour of the cell. This model is continually refined to improve our systems level understanding and to incorporate more mechanistic details.
Sensing and response in Halobacterium is the only example where the structure and dynamics of a signaling network has been studied in-depth within the archaeal branch of life.
 |
Robert Schulz und Ulrich Kleinekathöfer
School of Engineering and Science, Jacobs University Bremen, Germany
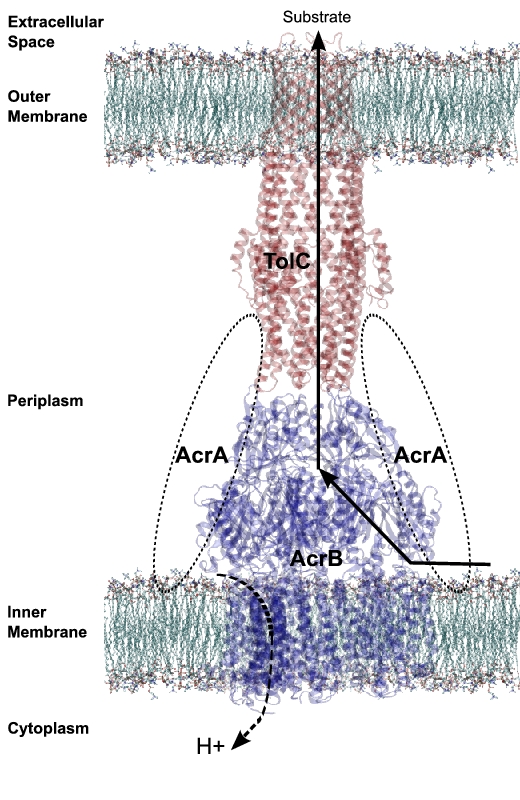
Bacteria, such as E. coli, use multidrug efflux pumps to export toxic
substrates through their cell membranes. The RND transporter of the
AcrAB-TolC efflux pump is able to export structurally and chemically
different substrates. This is one reason of the increasing antibiotic
resistance of bacteria. The effects of conformational changes on the
extrusion of drugs, which have been placed into one of the proposed
binding pockets, are assessed using different computational
methods within NAMD like targeted molecular dynamics. Previously, the
conformational changes of TolC which lead to an opening of the aperture
have been investigated.
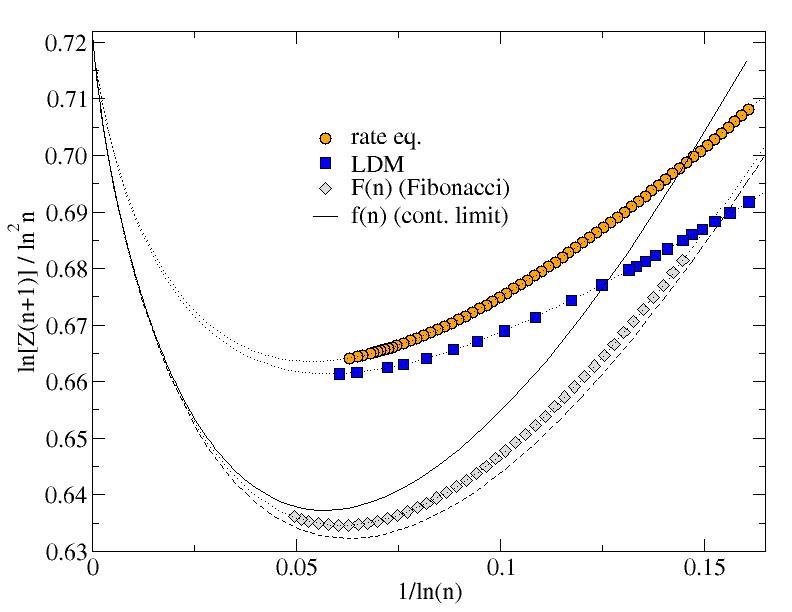 |
Stefan Boettcher1 and Stephan Mertens2,3
1Department of Physics, Emory University, Atlanta GA 30322-2430, U.S.A.
2Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
3Santa Fe Institute, 1399 Hyde Park Road,
Santa Fe, New Mexico 87501, U.S.A.
The Karmarkar-Karp differencing algorithm is the best known polynomial time heuristic for the number partitioning problem, fundamental in both theoretical computer science and statistical physics. We analyze the performance of the differencing algorithm on random instances by mapping it to a nonlinear rate equation. Our analysis reveals strong finite size effects that explain why the precise asymptotics of the differencing solution is hard to establish by simulations. The true asymptotics is obtained by a combination of numerical simulations and analytic arguments. Our calculations reveal subtle relations between the algorithm and Fibonacci-like sequences, and we establish an explicit identity to that effect.
The differencing algorithm is a nice example of a system for which the asymptotics cannot be determined by numerical simulations despite the fact that the system can be simulated very efficiently.
 |
Hannsjoerg Freund, Tobias Heidig
Max Planck Institute for
Dynamics of Complex Technical Systems, Sandtorstr. 1
39106 Magdeburg,
Germany
Open-cell foams are possible candidates for catalyst support in chemical engineering. They offer a higher mechanical strength and lower pressure drop in comparison to conventional randomly packed fixed-bed reactors. The influence of differences in local geometry on global parameters like pressure drop or velocity distribution is not yet fully understood.
In this study CFD-simulations of two foam-structures with different pore density were accomplished using the Lattice-Boltzmann-method. The LBM is a mesoscopic method capable for fluid simulations at low Reynolds-numbers. As a simulation result values for the global and local friction coefficient at different Re-numbers were obtained and the spatial distributed velocity field was calculated.
 |
Stephan Mertens
Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
May-September 2005
The stable matching problem is a prototype model in economics and social sciences where agents act selfishly to optimize their own satisfaction, subject to mutually conflicting constraints. The best known example is the stable marriage problem, where the agents are n men and n women that compete with each other in the ``marriage market''. Each man ranks all the women according to his individual preferences, and each woman does the same with all men. Everybody wants to get married to someone at the top of his or her list,but mutual attraction is not symmetric and frustration and compromises are unavoidable. A minimum requirement is a matching of men and women such that no man and woman would agree to leave their assigned partners in order to marry each other. Such a matching is called stable since no individual has an icentive to break it.
A stable matching in general is a pairing of adjacent vertices in a graph such that no unpaired vertices prefer each other to their partners under the matching. The corresponding graph in the stable marriage problem is bipartite, but there are many applications where the graph is non-bipartite. A well known example is the stable roommates problem, the problem to assign students of the same sex to the double bedrooms in a dormitory. A major difference between a bipartite and a non-bipartite matching problem is that the former always has a solution but the latter may have none.
We use Tina to measure the probability Pn that a random instance of a stable matching problem admits a solution. Large scale simulation indicate that Pn decays like n-1/4 for the stable roommates problem, i.e. on complete graphs. We also measured Pn for regular grids and Erdös-Renyi random graphs.
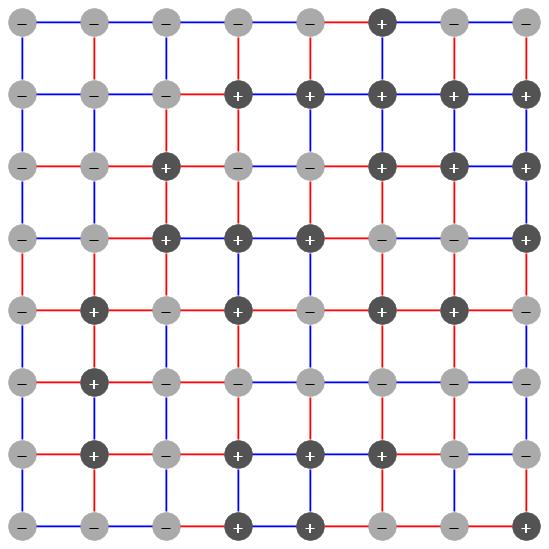 |
Heiko Bauke and
Stephan Mertens
Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
Ongoing
An Ising spin glass is a model for certain magnetic alloys. Imagine a set of N elementary magnets or spins, where each spin can either point up or down. Some spins interact with each other, others don't. The interaction between two spins can either be positive or negative. Spins that interact via a positive bond want to point in the same direction, spins with a negative bond want to point in opposite directions. In general there is no configuration of spins that satisfies all bonds, a phenomenon called frustration. The groundstate of a spin glass is a configuration of spins that minimizes the frustration, i.e. the number of violated bonds.
Finding the groundstate of a spin glass is equivalent to solving the Max-Cut problem from combinatorial optimization. This problem is NP-hard, i.e. there is no algorithm that is significantly better than exhaustively trying all 2N spin configurations. This exponential growth limits the size of solvable systems to rather small values of N, but clever algorithms nevertheless do find exact groundstates in reasonable time even for systems with thousands of spins. You can even solve your specific spin glass problem by sending an email to the Cologne spin-glass server.
We are currently working on a new algorithm for the spin glass problem. The first experiments
are very promising but it is not clear whether our algorithm can compete with the
branch and cut algorithms that are used by the
spin-glass server.
 |
Stephan Mertens1,
Marc Mézard2 and
Riccardo Zecchina3
1Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
2Laboratoire de Physique Théorique et Modeles Statistiques,Université de Paris Sud, Orsay, France
3The Abdus Salam International Centre for Theoretical Physics, Trieste, Italy
September 2003
The K satisfiability problem (K-SAT) is a fundamental problem from computer science. It is the problem to decide whether a formula of N Boolean variables can be satisfied, i.e. evaluated to TRUE by an assigment of the variables. Without loss of generality one can assume that the formula is organized as conjunction of clauses, where each clause is a disjunction of K variables or their negation. For K>2, this problem is NP-complete. K-SAT is a very important problem in theoretical computer science (some people would even say: the most important problem), but it has numerous practical applications as well. Try www.satlive.org as a gateway into the world of this fascinating problem.
Each clause represents a constraint that excludes 1 out of 2K of the possible assignments and the whole formula is satisfiable if the number of clauses is small compared to the number of variables, but unsatisfiable if the number of clauses is large.
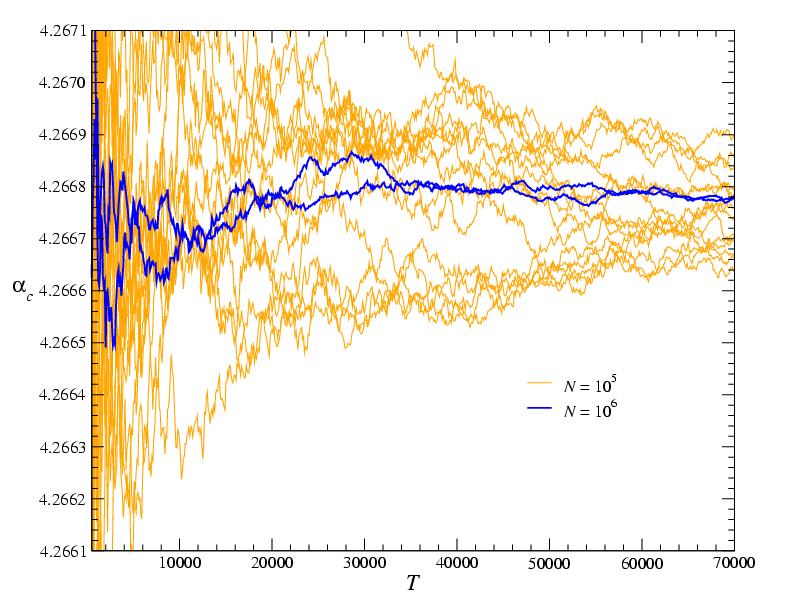
In random K-SAT, the variables are chosen independently for each clause, and a chosen variable appears pure or negated with probability 1/2. If M denotes the number of clauses, one observes that the ratio a=M/N is a control parameter that triggers a phase transition. There is a critical value ac such that a typical random formula is satisfiable if a < ac, but unsatisfiable if a>ac. The transition gets sharp in the limit N, M to infinity, and the value of transition point ac depends on K. This phase transition has been and still is in the center of interdisciplinary research that joints computer science, discrete mathematics and theoretical physics.
Using the cavity method from statistical mechanics, we derived precise numerical values for the transition points ac(K). The cavity approach yields a complicated set of coupled integral equations that needs to be solved numerically. The precise numerical values for ac(K) that were obtained using Tina's computing power could be compared to an analytical solution of the cavity equations in terms of a series expansion. It turns out that the series converges rather fast, hence the problem of locating the phase transition in random K-SAT might be considerd solved.
 |
Heiko Bauke1,
Christian Borgs2,
Jennifer Chayes2,
Stephan Mertens1 and
Boris Pittel3
1Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
2Microsoft Research, Redmond, U.S.A.
3Department of Mathematics, Ohio State University, Columbus, U.S.A.
Ongoing
The number partitioning problem (NPP) is defined as follows: Given a set of n non-negative, integer numbers a[1],a[2],...,a[n], divide this set into two subsets such that the sums of the numbers in each subset are as nearly equal as possible.
Partitioning is of both theoretical and practical importance. It is one of Garey and Johnson's six basic NP-complete problems that lie at the heart of the theory of NP-completeness. Among the many practical applications one finds multiprocessor scheduling and the minimization of VLSI circuit size and delay.
NPP displays a phase transition in its computational complexity: As long as n is smaller than the number of bits needed to encode the a[i]'s, the computational costs grow exponentially with n. If n exceeds this value, the computational costs decrease dramatically, and for even larger values, the costs grow again, but only linearly. This phasetransition and other surprising properties of the NPP are in the focus of our research.
See Brian Hayes' article " The easiest hard problem" in the March-April issue of American scientist for a very enjoyable introduction into this problem. The research papers are
 Heiko Baukeand
Stephan Mertens
Heiko Baukeand
Stephan Mertens
Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
Ongoing
All Monte Carlo simulations include some sort of averaging independent samples, a calculation that can be perfectly parallelized. Hence it is no surprise that more and more large scale simulations are run on parallel systems like networked workstations. In a parallel environment, the quality of a random number generator is even more important in a non parallel environment, to some extent because feasible sample sizes are easily 10...104 times larger as on a sequential machine. The main problem is the parallelization of the RNG itself. We introduce a class of random number generators called YARN (yet another random number). YARN generators are based on multiple linear congruences and exponentiation in prime number fields. They have a solid mathematical and empirical foundation, and they are efficient in sequential and in parallel simulations. Their statistical properties are excellent.
The YARN-generators and others random nuber generators have been
implemented in the C++ library TRNG (Tina's Random Number
Generators) which we make public available under the terms of GPL. You may
download the latest version of TRNG from the web side
TRNG.
The TRNG library has an object oriented easy to use design and is
highly speed optimized.
Research papers are
 |
Heiko Baukeand
Stephan Mertens
Institute for Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
Ongoing
Binary sequences of +1 and -1 with low autocorrelations have many applications in communication engineering. Their construction has a long tradition, and has turned out to be a very hard mathematical problem.J. Bernasconi introduced an Ising spin model that allows to formulate the construction problem in the framework of statistical mechanics.
The Bernasconi model is completely deterministic in a sense that there is no explicit or quenched disorder like in spin-glasses. Nevertheless the ground states are by definition highly disordered. This self-induced disorder resembles the situation in real glasses. In fact, the Bernasconi model exhibits features of a glass transition like a jump in the specific heat and slow dynamics and ageing.
The usual analytical and numerical tools of statistical mechanics have very limited applicability for the Bernasconi model. Exhaustive and partial enumerations seem to be the only means to get reliable results. We have applied Tina to find exact groundstates for systems up to size 58, i.e. we have exhaustively enumerated 258 configurations. Partial enumerations and heuristic searches will yield results for systems larger than 100 elements.
More informations and some references can be found
here.
 |
Peter Kohlert and
Klaus Kassner
Institute of Theoretical Physics, Otto-von-Guericke Unversität,
Magdeburg, Germany
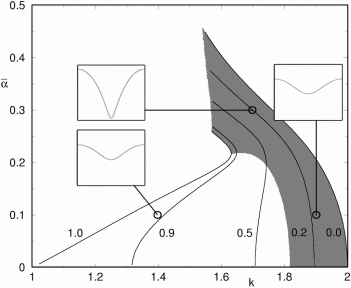
The Grinfeld instability is a mechanism which leads to structures on solid surfaces. In the presence of strain in the solid and of a suitable transport machanism for surface atoms, a re-arrangement of the surface due to energetic competition between elastic relaxation and creation of surface (and further factors) takes place. In the case of uniaxial stress the emerging patterns are sinusoidal waves which grow to cycloid-like structures which are flat on top and sharp in the valleys, where the elastic energy concentrates. Finally, the instability can lead to finite time-cusp singularities. For more complex pre-stress scenarios also diamond patterns and possibly hexagons are to be expected.
In this project we are interested in the manifold of stable surfaces away from the plane solution, in the special case of uniaxial strain and a semi-infinite solid. While this problem is easy to treat by a simple cosine series ansatz for very small amplitudes, it turns out that for mean square amplitudes larger than 0.15 the valleys become too sharp to be reasonably described by a moderate number of modes. Even spectral methods, as found in literature, fail to correctly describe the shape and position of the cusp singularity and miss a considerable part of the solution.
A generalization of the cycloids which we call multicycloids bears a multitude of advantages. First, the elastic energy density along such a curve can be calculated exactly, without any assumption of smallness of a parameter. Second, the variety of curves trackable by a multicycloid contains single and multiple cusps and even multivalued shapes which brings the later stages of a variety of structure creating processes closer to analytic description.
A related Paper can be found at
cond-mat/0208297.
 |
Alexander K. Hartmann
Department of Physics, University of California, Santa Cruz, U.S.A.
August 2001
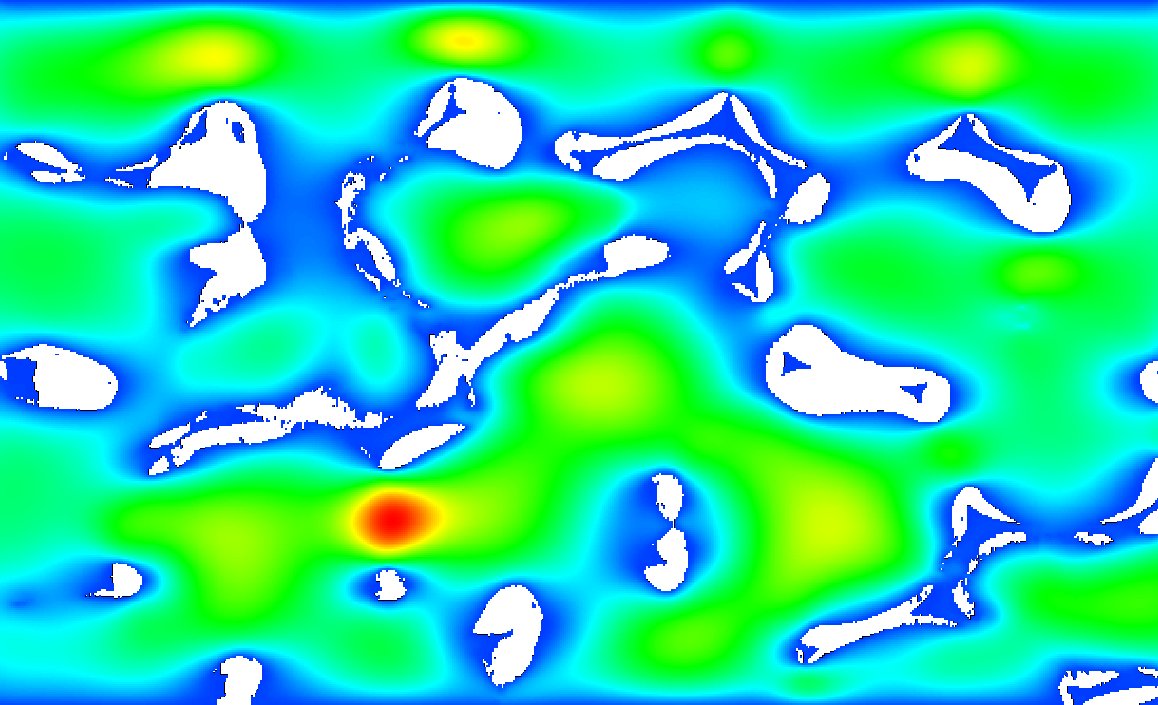
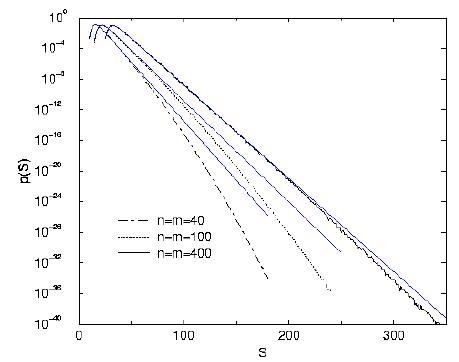
Modern molecular biology, e.g. the human genome project, relies heavily on the use of large databases, where DNA or protein sequences are stored. The basic tool for accessing these databases and comparing different sequences is a sequence alignment. The result of each comparison is an maximum alignment score S. To estimate the significance of the result of a comparison, one has to know, based on a random model, the statistical distribution p(S) of scores. Unfortunately, the region interesting region of p(S), where p(S) is very small (like p(S)~1e-40), is not known.
Here, a new method to calculate probability distributions in regions where the events are very unlikely is applied. The basic idea is to map the underlying model on a physical system. The system is simulated at low temperature, such that preferably configurations with originally low probabilities are generated. Since the distribution of such a physical system is known, the original unbiased distribution can be obtained. The result of the application to the sequence-alignment problem is shown in the figure.
A more detailed description of the outcome of this study can be found in a
preprint.
More information is available on the homepage of
Alexander K. Hartmann.
 |
 |
Eckard Specht1 and
Péter Gábor Szabó 2
2
1Institute of Experimental Physics, Otto-von-Guericke-Universität, Magdeburg, Germany
2Cygron Research and Development Ltd, Szeged, Hungary
Ongoing
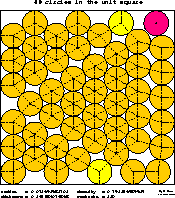
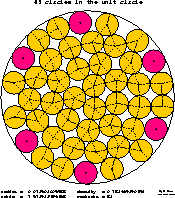
In sciences, engineering and real life several problems lead to the question of finding the densest packing of equal objects in a bounded box of special geometrical shape. For example:
Problems of this kind are exactly solvable only for some special cases. To get conjectured optimal packings, tochastic algorithms have to be applied.
One of the authors has written a public-domain program using a simple geometrical approach: Starting from randomly spread small circles, blow them up until collisions occur. Shake the whole configuration over and over again. This "brute force" billiards method lead to excellent packings not published in literature yet.
If you are interested in this topic, please refer to the author's page
packomania.
There are calculation forms for applications too.
Eckard Specht and
Péter Gábor Szabó.
 |
Phase transitions (like the liquid-gas transition for a fluid) are a central subject studied in statistical physics. The phase transitions in pure systems, like ideal gases, are already relatively well understood. The critical behavior of all physical quantities can be described via critical exponents.In contrast, phase transitions in systems with (quenched) disorder exhibit many puzzles
In theoretical physics, the random-field Ising model (RFIM) is a widely studied prototypical disordered system. It is believed to behave in the same manner like the diluted antiferromagnet in a field, which can be studied experimentally.
Here, the ferromagnet-to-paramagnet transition of the four-dimensional RFIM with Gaussian distribution of the random fields is studied. Exact ground states (i.e. of temperature T=0) of systems with sizes up to 32x32x32x32 particles are obtained using modern and fast graph theoretical algorithms. The magnetization, the disconnected susceptibility, the susceptibility and a specific heat-like quantity are calculated.
A more detailed description of the outcome of this study can be found in a
preprint.
Further information is available on the homepage
of
Alexander K. Hartmann.
 |
Alexander K. Hartmann and
A. Peter Young
Department of Physics, University of California, Santa Cruz, U.S.A.
June/July 2001
The behavior of disordered systems shows a much richer behavior than ordered physical systems (like cristalls). Despite much efforts in the past, they are not fully understood yet.
A spin glass is a disordered magnetical system, one of the standard models in statistical physics. It consists of mixtures of magnetic and non-magnetic materials, e.g. a small fraction of iron in gold. In biology, neural networks behave according the same principles. For theoretical studies, abstract models are used, where the systems are made of simple particles, so called Ising spins, which can take only two states "up"/"down".
One of the open questions under consideration is, whether two-dimensional Ising spin glasses exhibt and ordered phase at finite temperature. In this project the question was addressed via exact ground-state calculations using modern algorithms from graph theory. By disturbing the system, domain walls are introduced into the system, and the system size-dependence of the domain-wall energy is studied. For this purpose one must average over many realizations of the disoderer, typically 10000 samples. Here, much larger system sizes than before, up to 480x480 spins, where studied. This huge numerical effort requires a parallel computer like Tina and allows for results which have not been found so far.
A description of the outcome of this study can be found in a
preprint.
More information is available on the homepages
of
Alexander K. Hartmann and
A. Peter Young.
URL: http://tina.cryptoweb.de
Sunday, January 11th 2026, 12:21:27 CET